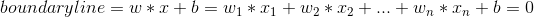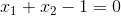Classification via Single Layer Logic Perceptrons
In my previous post on ANNs, I explained that a perceptron is the main building block of a neural network. In this post, I will show you how basic, logical operator perceptrons can be used for classification.
Simple Linear Classification
For the sake of simplicity, let's use a simple linear classification problem.
In the above example, there are 2 visible classes: blue and red. They are separated by a boundary line that is defined by:
x is your input vector, w is your weights vector and their product is a dot product (NOT an element wise product). b is your bias.
We would like our perceptron to output a class for any given point: red or blue. Let's give red and blue numeric representations: red = 1, blue = 0.
If our point is above the boundary line, in the positive space, is will be classified as 1.
If our point is below the boundary line, in the negative space, it will be classified as 0.
The above equation is called a step function, which is just a discontinuous function (non differentiable), whose output moves from one constant to another.
Logical Operator Perceptrons
The 2 most basic single layer perceptrons, also referred to as single layer feedforward neural networks, are the AND and OR perceptrons (think boolean operators). Depending on which one you're using, the boundary line varies.
AND Perceptron
The AND perceptron requires that all input neurons be activated for the output to equal 1; this means that all inputs (x) must = 1. If one or more of the inputs = 0, the output is also 0.
Take a look at this simple example below, where the weights vector = [0.5,0.5] and the bias = -1.
When both neurons are activated (equal to 1), the output of the equation is 0, and in turn our perceptron's output is 1.
When one or more neurons are not activated (equal to 0), the output of the equation is negative, and in turn our perceptron's output is 0.
OR Perceptron
The OR perceptron requires that at least one neuron be activated for the output to equal 1; this means that only 1 of the inputs (x) must = 1. If all inputs = 0, the output is also 0.
Take a look at this simple example below, where the weights vector = [1,1] and the bias = -1.
When at least 1 neuron is activated (equal to 1), the output is equal to or greater than 0, and in turn our perceptron's output is 1.
When both neurons are not activated (equal to 0), the output of the equation is -1, and in turn our perceptron's output is 0.
Below are plot visuals of 3 logical operator perceptrons. The white points are of the positive class and the black points are of the negative class.
Bonus: NAND (NOT) Perceptron
The NAND perceptron is truly the opposite of the AND perceptron, hence the name: NOT AND, and requires that at least one neuron be deactivated for the output to equal 1; this means that 1 or more of the inputs (x) must = 0. If all inputs = 1, the output is 0.
Take a look at this simple example below, where the weights vector = [-1,-1] and the bias = 1.
When at least 1 neuron is deactivated (equal to 0), the output is equal to or greater than 0, and in turn our perceptron's output is 1.
When both neurons are activated (equal to 1), the output of the equation is 0, and in turn our perceptron's output is 0.
More complex boundary equations can be specified, depending on our classification needs. Perceptrons can also be combined to create multi-layer perceptrons. Logical operator perceptrons are quite powerful as we are able to, using various combinations, construct any logical function and in turn, deconstruct and understand complex logical functions. One of the most beautiful (and simple) examples is the XOR perceptron, which combines an AND perceptron, a NAND perceptron and an OR perceptron to create a non-linear classifier. The XOR perceptron will be the subject of one of my next posts.